说明

时间限制：1 Sec 内存限制：256 MB 输入文件：prodigy.in 输出文件：prodigy.out

小明得到了一棵由顶点 $1,2,...,N$ 构成的树 $T$。树 $T$ 的每个顶点 $i$ 上都已经写有数值 $i$。

小明决定将树 $T$ 视为有根树来玩游戏。

对于有根树，小明定义：当顶点 $i$ 上写的数值大于其所有祖先（不包含自身）顶点上的数值时，顶点 $i$ 称为神童。特别地，根节点一定是神童。

小明将 $N$ 个顶点中神童的数量定义为神童数。（请注意：每个顶点是否为神童，取决于选择哪个顶点作为根节点）

例如考虑下图所示的有根树，黄色顶点是神童，神童数为 $4$。

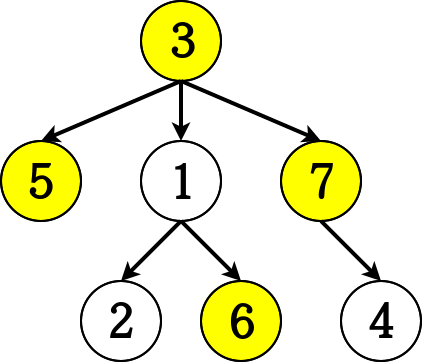
其中写有数值 $6$ 的顶点是神童，因为它的祖先顶点数值为 $\{3,1\}$，均小于 $6$；

而写有数值 $4$ 的顶点不是神童，因为它的祖先顶点数值为 $\{3,7\}$，包含比 $4$ 大的数值。

小明发现树 $T$ 的神童数会随根节点的选择而变化，因此他向你询问：对于每个顶点 $i (i=1,2,...,N)$ 作为根时的神童数 $S_i$ 是多少。

由于需要给出的数值太多，小明要求你计算数列 $r=\{r_1,r_2,...,r_N\}$ 对应的乘积：$(r_1+S_1) \times (r_2+S_2) \times ... \times (r_N+S_N)$，并将结果对 $10^9+7$ 取模后告诉他。

输入格式

第一行输入树的顶点数 $N$；

第二行输入用于计算答案的数列 $r$ 的 $N$ 个元素（空格分隔）；

接下来 $N-1$ 行，每行输入两个整数 $u, v$，表示树 $T$ 中连接顶点 $u$ 和 $v$ 的无向边。

注意：输入数据量可能较大，请留意处理效率。

输出格式

输出 $\prod_{i=1}^N(r_i+S_i) \mod (10^9+7)$ 的结果，占一行，末尾需换行。

样例

样例 1

3
0 0 0
1 2
2 3

6

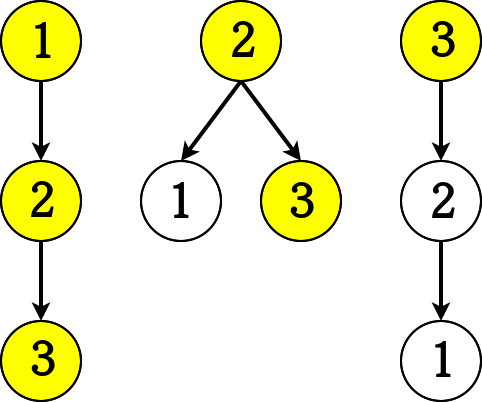
样例说明：

以顶点 $1$、$2$、$3$ 分别为根时的神童数依次为 $3$、$2$、$1$，乘积为 $(0+3)×(0+2)×(0+1)=6$。

样例 2

3
0 0 0
1 3
3 2

4

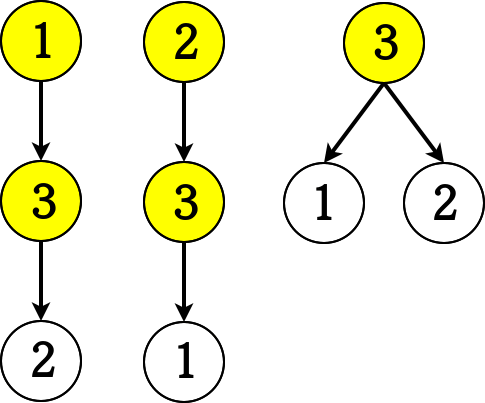
样例说明：

以顶点 $1$、$2$、$3$ 分别为根时的神童数依次为 $2$、$2$、$1$，乘积为 $(0+2)×(0+2)×(0+1)=4$。

样例 3

20
397391841 679700971 145606697 977415091 513786611 99670444 666370425 151199845 823785563 113697511 311512752 592551093 141690528 337950684 441783513 543190271 462296398 851050627 141769971 473127767
17 19
18 11
19 6
20 8
8 16
20 3
13 9
11 10
15 8
11 20
17 18
14 8
1 20
2 5
11 7
11 4
5 20
1 12
2 13

598344873

样例说明：

需注意结果需对 $10^9+7$ 取模。

数据范围

对于 24% 的数据，$N \le 3000$。

另有 24% 的数据，输入的树是一条链。

对于 100% 的数据，$1 \le N \le 2\times 10^5$，$0 \le r_i \lt 10^9+7$，$1 \le u_i,v_i \le N$。

对于 100% 的数据，输入的图保证是一棵包含 $N$ 个顶点的树。