说明

时间限制：1 Sec 内存限制：256 MB 输入文件：cost.in 输出文件：cost.out

A 国中有 $N $ 个城镇和 $ M $ 条道路，城镇编号为 $1 \sim N$，道路编号为 $1 \sim M$。道路连接的城镇之间可以双向通行。任意两个城镇之间不存在两条及以上的道路，且道路的两端不会是同一个城镇。初始状态下，任意一个城镇都能通过若干条道路到达其他所有城镇。

A 国每年都会为每条道路产生相应的维护费用。作为国王的你，考虑关闭部分道路以削减维护费用。道路关闭后，将无法通过该道路往返城镇，但能节省该道路对应的维护费用。但为了避免国民反对，道路关闭后必须保证所有城镇依然连通——即任意一个城镇都能仅通过未关闭的道路到达其他所有城镇。

此外，A 国的国民指定了 $ K $ 条道路，他们对这些道路有特殊感情，要求不得关闭。

你需要在满足国民要求的前提下，尽可能最大化削减的维护费用总和。请计算能削减的维护费用总和的最大值。

输入格式

第一行包含三个整数 $N$、$M$、$K$，以空格分隔；接下来 $M$ 行，每行描述一条道路的信息：第 $i$ 行包含三个整数 $a_i 、 b_i 、 c_i$，分别表示道路 $i$ 连接的两个城镇、道路 $i$ 的维护费用；最后 $K$ 行，每行包含一个整数 $e_i$，表示国民要求不得关闭的道路编号，保证 $e_1 < e_2 < \dots < e_K$。

输出格式

输出能削减的维护费用总和的最大值。

样例

样例 1

5 6 3
1 2 8
1 3 5
2 3 7
2 4 4
3 5 4
4 5 7
1
2
3

7

样例说明：

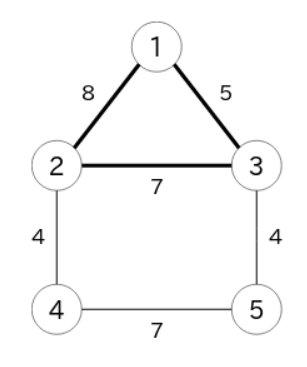
道路 $1$、$2$、$3$ 不得应民众要求关闭。道路 $4$、$5$、$6$ 中，若关闭 $2$ 条及以上，城镇 $4$ 和城镇 $5$ 将会陷入孤立状态。在这种情况下，关闭道路 $6$ 是最优选择。由于道路 $6$ 的维护费用为 $7$，因此可削减的维护费用总和最大值为 $7$，输出结果为 $7$。

样例 2

4 5 0
1 2 5
1 3 3
1 4 1
2 3 2
2 4 3

8

样例说明：

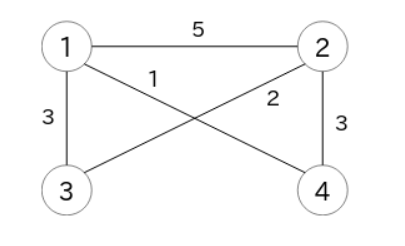请注意，$K=0$ 的情况也是可能出现的。

通过关闭道路 $1$，以及道路 $2$ 或道路 $5$ 中的任意一条，可削减的维护费用总计为 ( 5+3=8 )。

这是可削减维护费用总和的最大值，因此输出 $8$。

样例 3

6 11 6
4 5 15
2 5 14
2 6 10
1 6 15
3 6 11
2 3 18
5 6 12
1 4 4
2 4 6
1 2 17
3 5 6
1
3
6
7
10
11

50

数据范围

对于 35% 的数据，满足 $N \le 10$，$M \le 20$。对于 100% 的数据，满足 $1 \le N \le 10^5$，$N-1 \le M \le \min(N \times (N-1)/2, 10^5)$，$0 \le K \le M$，$1 \le e_1 < e_2 < \dots < e_K \le M$。对于 100% 的数据，保证初始图为连通图，对于 $i=1,2,\dots,M$ 满足 $1 \le a_i < b_i \le N$ 且 $1 \le c_i \le 10^9$，对于 $i \neq j$ 满足 $(a_i, b_i) \neq (a_j, b_j)$。